【矩阵】奇异值分解
特征值
对于方阵$\mathbf{A}$,在几何意义上可以表示成线性变换(基变换)。例如:
$$
\mathbf{A} = \begin{pmatrix}
1 & 2 \\
3 & 4
\end{pmatrix}
$$
我们考虑一个圆。在这个圆中,所有的矩阵乘都可以简单理解为对这个圆的“挤压”和“翻转”。那很自然的想到,把这个圆变换成“椭圆”,那在长轴和短轴部分是不会“旋转”的,只有简单的“伸缩”。并且我们只需要知道长轴和短轴的伸缩程度,就可以知道这个线性变换的全部信息。
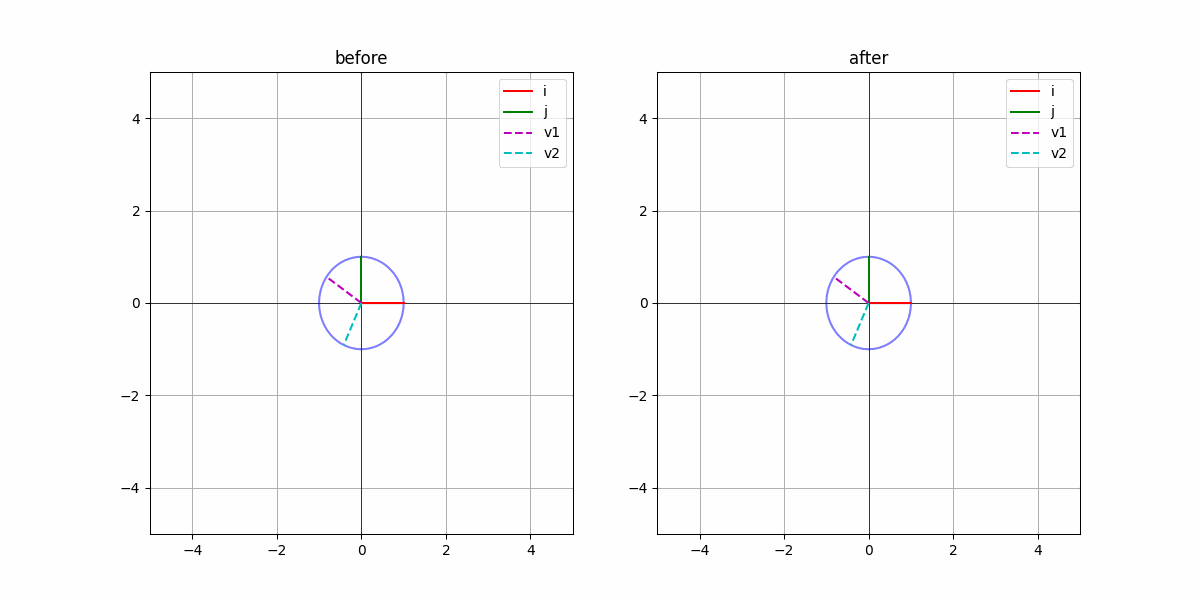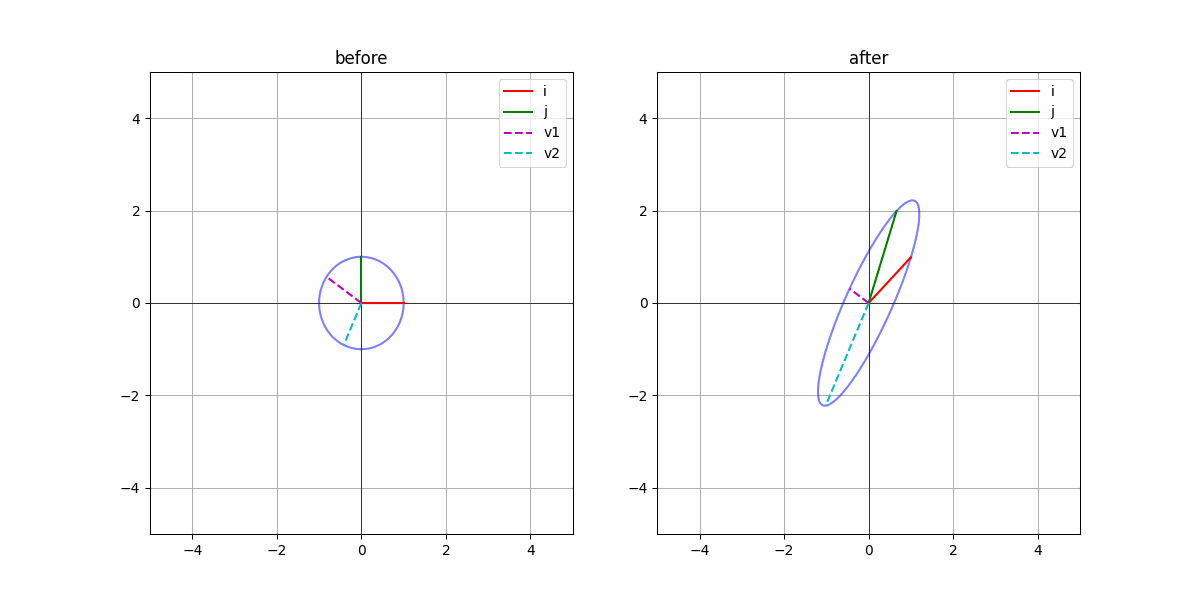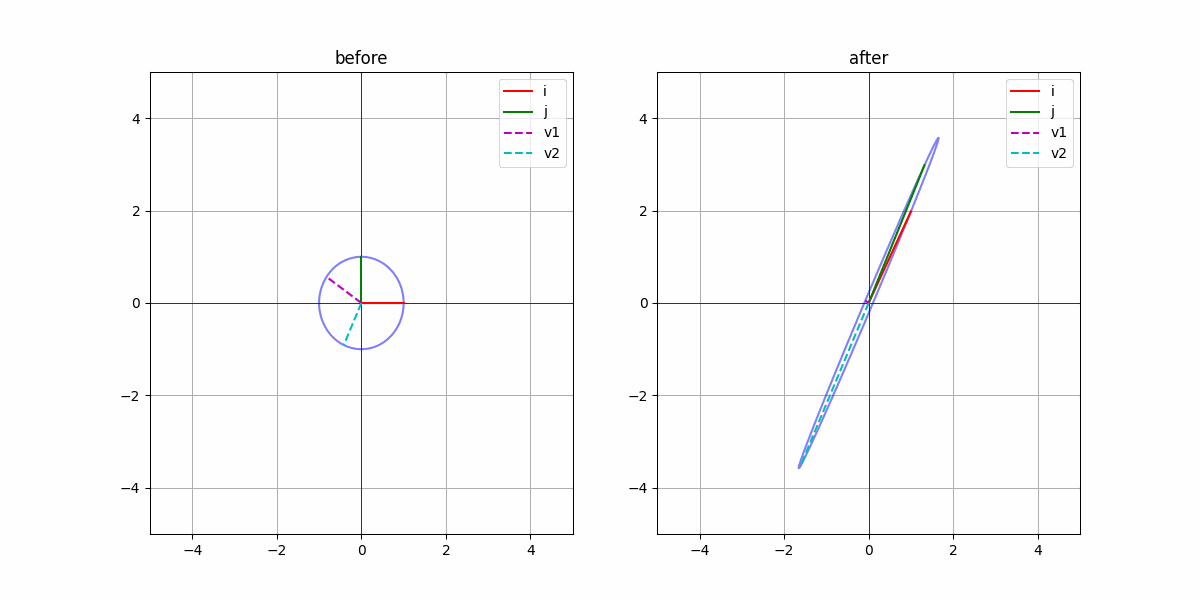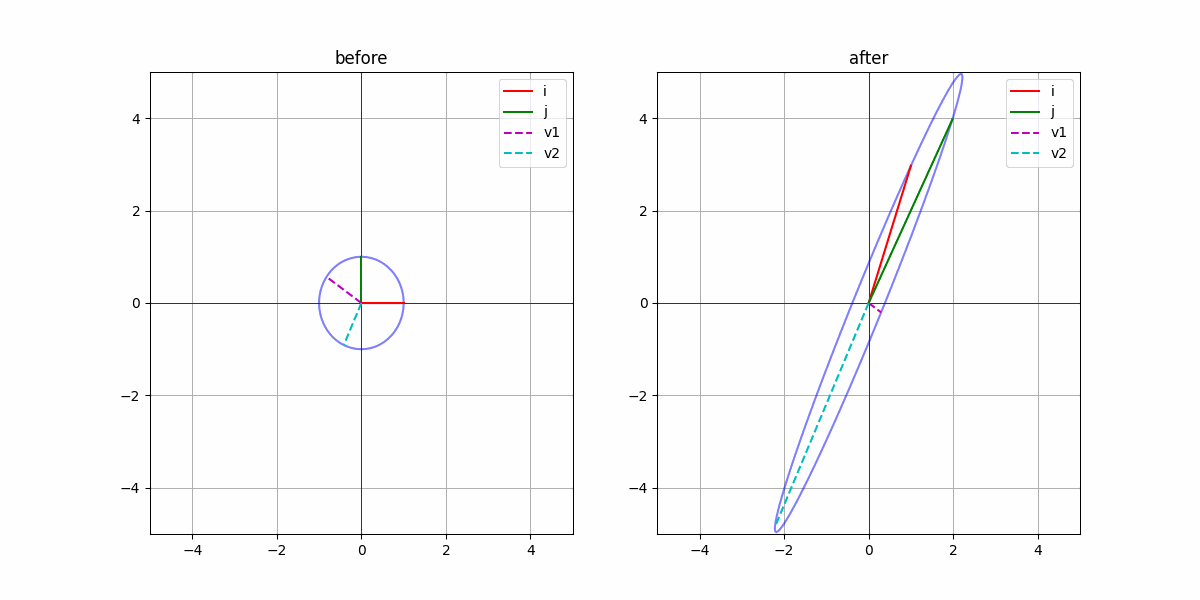
因此,我们把单位长度的长轴和短轴称为特征向量$\mathbf{v}$,而长轴和短轴的模称为特征值$\lambda$。
这里我们通过 python 的 numpy 库来计算特征值和特征向量:
# 定义矩阵A A = np.array([[1, 2], [3, 4]]) # 计算特征值和特征向量 eigenvalues, eigenvectors = np.linalg.eig(A)
特征值为:
$$
\lambda_1 = -0.3723, \lambda_2 = 5.3722
$$
特征向量为:
$$
\mathbf{v}_1 = \begin{pmatrix}
-0.82456484 \\
0.56576746 \\
\end{pmatrix}, \mathbf{v}_2 = \begin{pmatrix}
-0.41597356 \\
-0.90937671 \\
\end{pmatrix}
\\
\mathbf{P} = \begin{pmatrix}
\mathbf{v}_1 & \mathbf{v}_2
\end{pmatrix}
$$
因此这个变换$\mathbf{A}$可以由特征向量的伸缩完全表示:
$$
\mathbf{A}\mathbf{P} = \mathbf{P}\mathbf{D} \Rightarrow \mathbf{A} = \mathbf{P}\mathbf{D}\mathbf{P}^{-1}
$$
如果$A$是正交矩阵,那不存在实数特征值。
特征值分解
基于上面的案例,我们考虑泛化的情况。有方阵$\mathbf{A} \in \mathbb{R}^{n \times n}$,特征值分解为:
$$
\mathbf{A} = \mathbf{P}\mathbf{D}\mathbf{P}^{-1}
$$
而能够被特征值分解的矩阵,充分必要条件如下:有$n$个线性无关的特征向量。
